Un arbore în teoria grafurilor este un tip special de graf aciclic (fără cicluri) și conex (oricare două noduri sunt conectate printr-un drum). Structura unui arbore este de tip ierarhic, în sensul că există un nod special numit rădăcină și fiecare alt nod este legat de un singur nod părinte, cu excepția rădăcinii.
-
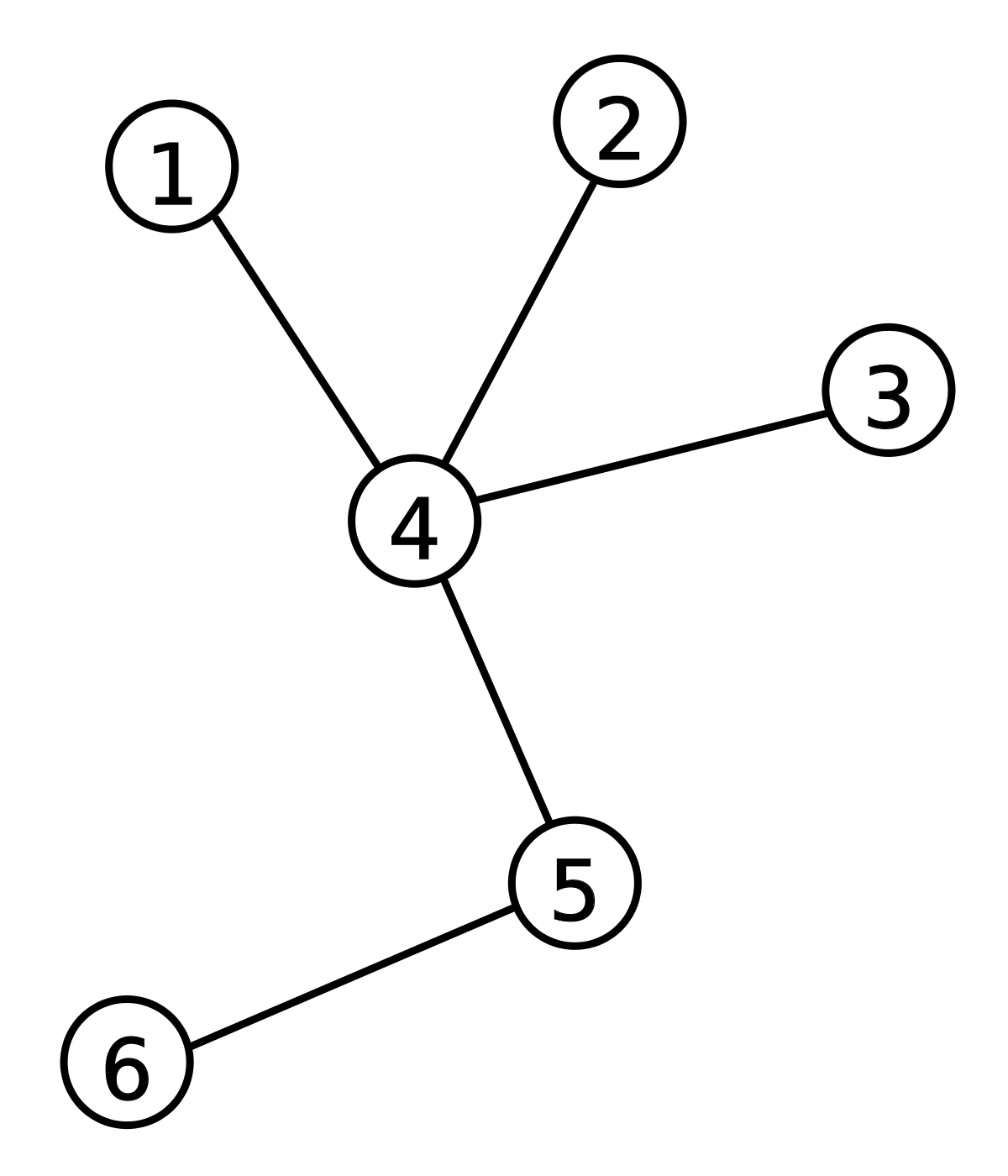
Noduri
- Reprezintă elementele individuale ale arborelui. -
Muchii
- Reprezintă legăturile dintre noduri. -
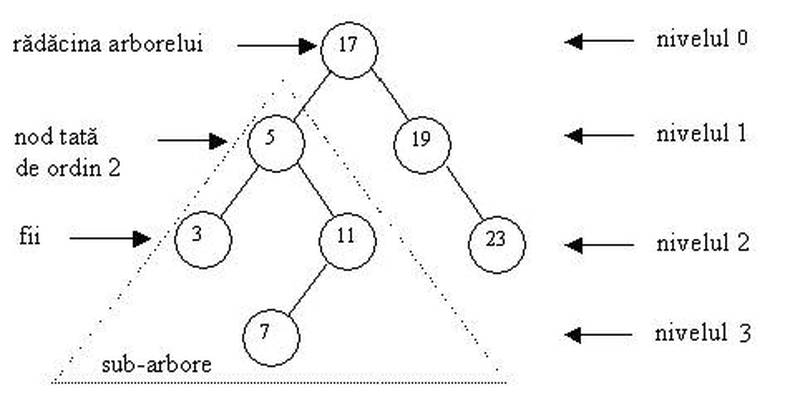
Rădăcină
- Nodul de bază al arborelui, care nu are niciun părinte. -
Frunze
- Nodurile fără niciun copil, situate la capătul de jos al arborelui. -
Noduri interne
- Nodurile care au cel puțin un copil. -
Subarbori
- Fiecare nod și descendenții săi formează subarbori. -
Nivele
- Nivelul unui nod este determinat de distanța sa de la rădăcină.
- Fiecare nod, cu excepția rădăcinii, are un singur părinte.
- Nu există cicluri sau drumuri ciclice în arbore.
- Există exact un drum între oricare două noduri din arbore.
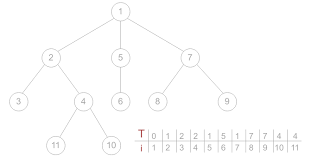
Arborii sunt creați prin vectorul de tați.
Elementul cu valoarea 0 în vector este rădăcina.
Fiecare valoare din vector este părintele
indicelui.
În exemplu din dreapta i reprezintă nodul, iar T părintele său.